Blog Details

• October 14, 2019
• No Comments
• Oilfield Knowledge Training Centre

NMR Introduction

The basic physical principle of NMR measurement relies on the fact that the molecular behaviour of certain materials can be affected by the action of a magnetic field. Just as a bar magnet can be aligned to a magnetic field, it is possible to align certain nuclei in a magnetic field.

These nuclei have two important properties:

1. Magnetic Moment – which determines the strength of the interaction between the nuclei and the magnetic field.
2. Spin – in a magnetic field, the nuclei spin which causes them to precess around the applied magnetic field.

The nuclear spins precess at a frequency that depends on the strength of the applied magnetic field. To put it another way, the nuclear spin possesses a resonance frequency that is related to the strength of the magnetic field, hence the term Nuclear Magnetic Resonance.

NMR is of interest to the petrophysicist because the behaviour of the nuclear spins is related to:

1. Fluid properties such as chemical composition and viscosity of the fluid.
2. Where a fluid is contained in a porous medium, the interaction of the nuclear spins with the pore surface perturbs the behaviour of the nuclear spins.

In rocks, the overall magnetization of a fluid is related to pore size and fluid composition.  By knowing the pore size distribution which is related to the T₂ distribution, it is possible to derive the bound fluid volume which can be used, in turn, to derive permeability.

Nuclei and Magnetic Fields

Only nuclei with an odd number of protons possess a magnetic moment i.e. the ability to interact with magnetic fields. In terms of nuclei encountered in formation evaluation, hydrogen protons have a large magnetic moment which allows the easy isolation of hydrogen in an NMR experiment. The nuclei also possess spin, and these spinning bar magnets can interact with an applied magnetic field (the B₀ field).

The NMR measurement used in the petrophysical analysis of rocks utilizes three different applied magnetic fields:

1. A static magnetic field, B₀.
2. A magnetic field generated using oscillating radio frequency (rf) pulses (B₁).  This field is applied normal (at right angles) to the static B₀.
3. Local magnetic field fluctuations generated by unpaired electrons and neighbouring nuclei.

Isolation of Hydrogen Nuclei

In an applied magnetic field, the protons precess with an angular frequency called the Larmor frequency (f₀) which is determined by the strength of the magnetic field (B₀) and the gyro-magnetic ratio (γ).

              f₀ = (γ/2π)* B₀  …………………………………………  Equation-1

By tuning the rf (radio frequency) of the NMR instrument to the Larmor frequency, the signal from hydrogen can be maximised.

Behaviour in Applied Fields

Without an applied magnetic field, the proton spins will exhibit random orientation (1).  When a magnetic field is applied, the spins align in the magnetic field B₀and begin to precess with frequency f₀ (2).

In fact, the protons align themselves both parallel and anti-parallel to the magnetic field (3).  This actually reflects protons in two different energy states.  The Boltzmann statistic predicts that, at room temperature, the number of spins in the lower energy level, N+, slightly outnumbers the number in the upper level, N- (i.e. slightly more aligned in one direction than the other):

               N-/N+ = e ^–E/kT ……………………………………….Equation2

where:

E          = Energy difference between spin states.

k          = Boltzmann’s constant, 1.3805x10e-23 J/Kelvin.

T          = Temperature in Kelvin.

N-        = Number of spins in upper energy level

N+        = Number of spins in lower energy level

The difference between parallel and anti-parallel magnetization is very small, therefore, the net magnetization is very small. This creates a problem for detecting the nuclei because the NMR signal is very small compared to B₀ and is in the direction of B₀.  Consequently, in the direction of B₀ the signal from the hydrogen protons is not easily detectable (4).

Detection of Nuclei Using Spin Tipping

From above we can be seen that proton spins cannot be detected by simply aligning them in the B₀ magnetic field.  To enable their detection, proton spins must be perturbed so that they are tipped out of the B₀field.  This spin tipping is achieved by disturbing the equilibrium of the aligned protons by applying another magnetic field, B₁, normal to the B₀ field.

This is achieved by applying an rf pulse tuned to the Larmor frequency at an angle of 90⁰ to the direction of B₀ (1). The applied B₁ field is used to tip the proton spins through 90⁰ and, as the B₁ field is generated by an rf pulse, it can be turned on and off, and the transition of the spins between the B₀ and B₁ field can be detected (2).

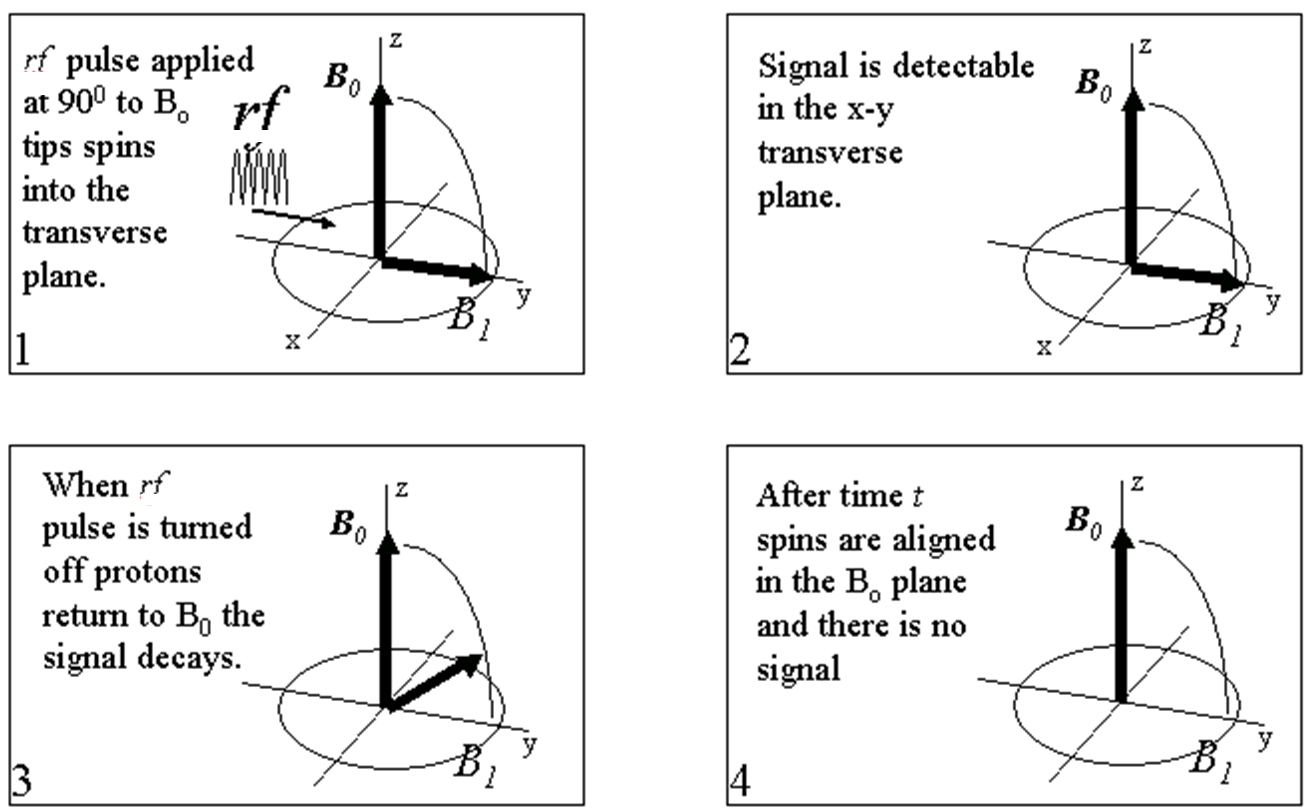
Spin tipping can be considered to be a four stage process:

1. An rf pulse is applied at 90⁰ to B₀ ; this tips the spins 90⁰ into the transverse plane.
2. When the rf pulse is turned off, proton spins in the transverse plane can be detected.
3. After the rf pulse is turned off, proton spins begin to return to alignment with B₀ and the signal decays.
4. After a certain time, t, the signal has completely decayed.

Detection of magnetization decay in the transverse plane is referred to as the ‘transverse relaxation’ or the ‘T₂ relaxation’. In the case of formation evaluation, the NMR experiment basically examines the time taken for the protons’ spins to relax from B₁ to B₀ by detecting magnetization in the transverse plane.

To discuss NMR technique with us in details kindly send us a note on support@oilfieldknowledge.com